
Handy Links
SLAC News Center
SLAC Today
- Subscribe
- Archives: Feb 2006-May 20, 2011
- Archives: May 23, 2011 and later
- Submit Feedback or Story Ideas
- About SLAC Today
SLAC News
Lab News
- Interactions
- Lightsources.org
- ILC NewsLine
- Int'l Science Grid This Week
- Fermilab Today
- Berkeley Lab News
- @brookhaven TODAY
- DOE Pulse
- CERN Courier
- DESY inForm
- US / LHC
SLAC Links
- Emergency
- Safety
- Policy Repository
- Site Entry Form

- Site Maps
- M & O Review
- Computing Status & Calendar
- SLAC Colloquium
- SLACspeak
- SLACspace
- SLAC Logo
- Café Menu
- Flea Market
- Web E-mail
- Marguerite Shuttle
- Discount Commuter Passes
-
Award Reporting Form
- SPIRES
- SciDoc
- Activity Groups
- Library
Stanford
Around the Bay
Subnuclear Scaling, Simplicity and Supersymmetry
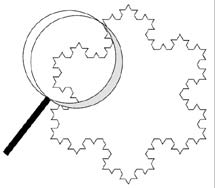 Imagine a world which looks exactly the same at every scale, no matter how much you magnify it. A simple representation of this kind of world is a fractal, like the Koch snowflake, which looks the same when magnified by any power of three.
Imagine a world which looks exactly the same at every scale, no matter how much you magnify it. A simple representation of this kind of world is a fractal, like the Koch snowflake, which looks the same when magnified by any power of three.
The world of atoms—as well as nuclei, protons and neutrons—has a definite size, so it doesn't behave like this. But at distances much smaller than the radius of the proton, quarks and gluons behave almost this way.
In the theory of QCD (Quantum ChromoDynamics), the interactions of quarks and gluons become weak at short distances. This property is known as asymptotic freedom. The interactions get weak quite slowly, however, so QCD is almost independent of scale.
The quasi-freedom of the quarks explained the dramatic "scaling" results of electron-proton scattering experiments performed at SLAC in the 1960s. But the scaling is not perfect, because residual interactions of the quarks cause them to change how they are distributed in the proton, as you look closer. The length of the curve around the Koch snowflake is an example of this phenomenon—when you look three times closer, the length increases by a factor of 4/3, because you see a new triangle where there was once a straight line.
In QCD, the numbers analogous to this factor of 4/3 are called anomalous scaling dimensions. These numbers were very important in the analysis of the scattering experiments at SLAC in the 1960s and 1970s, and they have remained important through the decades. They can be computed in an expansion in a small parameter, the QCD coupling. David Gross and Frank Wilczek computed the first term in the expansion, in one of the initial papers on asymptotic freedom. The next term was worked out by two groups in the late 1970s. The next order after that is called the three loop approximation.
That order was only completed two years ago. It took several years of work (in an heroic effort by Sven Moch, Jos Vermasen and Andreas Vogt) and thousands of hours of computer time, all to evaluate 9,018 Feynman diagrams. It would be nice if there were an easier way to get some of these numbers!
Now, there is an imaginary world which looks exactly the same at every scale. It is not quite QCD, but a related theory I'll call SQCD. (The S stands for supersymmetric, and in fact there are four different supersymmetries in this theory.) In this theory the coupling of the particles is always the same, no matter the scale. That was proved by Stanley Mandelstam and colleagues in the mid 1980s. Computing numbers in SQCD is much simpler than in QCD. For example, Zvi Bern, Volodya Smirnov and I showed last year how one of the three loop numbers for SQCD could be squeezed out by calculating just four integrals, which is a lot less work than 9,018 Feynman diagrams!
If this number for SQCD had nothing to do with QCD, this might be just an idle amusement. But there is a remarkable—yet poorly understood—relation between the sets of numbers, noticed by a group including Lev Lipatov. For example, one of the numbers in QCD turns out to be 67/18 – π2/6, while the corresponding number in SQCD is – π2/6. Here π = 3.14159... is the ratio of the circumference of a circle to its diameter. π is also known as a transcendental number.
The general rule is that, once you order the numbers according to how transcendental they are, then the "most transcendental" parts of the QCD numbers give you precisely the SQCD numbers.
Going back the other way, you can predict a definite piece of the QCD answer by doing a generally much simpler computation in SQCD. At the moment my colleagues, Zvi Bern, Michael Czakon, David Kosower, Volodya Smirnov, and I are working out the four loop number in SQCD. But we also want to know if there is any way to use the imaginary world of SQCD to find the rest of the pieces of the results for real-world QCD, namely the ones that have lesser amounts of transcendentality. Doing so may require some serious transcendental meditation.
—Lance Dixon
SLAC Today, October 5, 2006
Above image: The Koch snowflake. (Click on image for larger version.)